[문제]
분수 A/B는 분자가 A, 분모가 B인 분수를 의미한다. A와 B는 모두 자연수라고 하자.
두 분수의 합 또한 분수로 표현할 수 있다. 두 분수가 주어졌을 때, 그 합을 기약분수의 형태로 구하는 프로그램을 작성하시오. 기약분수란 더 이상 약분되지 않는 분수를 의미한다.
[입력]
첫째 줄과 둘째 줄에, 각 분수의 분자와 분모를 뜻하는 두 개의 자연수가 순서대로 주어진다. 입력되는 네 자연수는 모두 30,000 이하이다.
[출력]
첫째 줄에 구하고자 하는 기약분수의 분자와 분모를 뜻하는 두 개의 자연수를 빈 칸을 사이에 두고 순서대로 출력한다.
[예제]
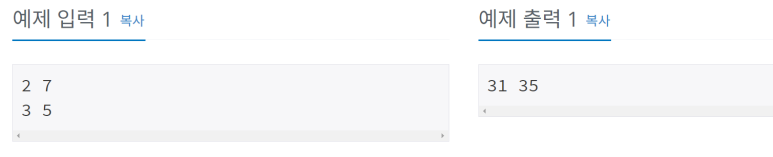
>문제 풀이
input))
분자1 분모1
분자2 분모2
이렇게 입력되면
c1/p1 과 c2/p2를 더하고 기약분수를 구해주면 됩니다.
나올 수 있는 최대수는 입력되는 분자 또는 분모가 30,000이하 이므로 9억 int 범위로 감당 가능합니다.
1) 분수의 합을 구하고
2) gcd를 구하여 기약분수를 만들어 출력한다.
gcd를 구할 때는 호제법을 사용한다.
> 유클리드 호제법이란?
gcd(A, B)= gcd(B, A%B)
* 증명
G를 A와 B의 최대공약수라고 할 때, A= aG, B= bG
A= Bq+r 니까
aG= bGq + r
r중심으로 정리하면 r = aG - bGq = (a-bq)G
B= bG , r= (a-bq)G 니까 G가 B와 r의 최대 공약수가 되려면 b와 (a-bq)가 서로소 임을 증명해야한다.
만약 서로소가 아니라고 가정을 해보자.
두 수가 서로소가 아니라면 b= mg , a-bq= ng 로 g라는 공약수가 존재한다.
b의 값을 오른쪽 식에 대입하면 a-mgq=ng
정리하면 a= (mq+n)g 이다.
우리는 처음에 A와 B 두 수를 A= aG, B= bG (G는 A와 B의 최대공약수) 라고 선언했는데, 즉 a와 b는 서로소라는 의미이다.
근데 아래 식에서 b= mg 이고 a= (mq+n)g 이면 a와 b는 공약수 g를 갖게된다.
따라서 b와 (a-bq)는 서로소이다.
>전체 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan= new Scanner(System.in);
int c1, c2, p1, p2;
//c1/p1, c2/p2
c1= scan.nextInt();
p1= scan.nextInt();
c2= scan.nextInt();
p2= scan.nextInt();
//더해주고
c1=c1*p2+c2*p1;
p1=p1*p2;
int gcd= getGcd(c1, p1); //최대공약수를 구해준다.
System.out.println(c1/gcd+" "+p1/gcd); //기약분수 출력
}//main
public static int getGcd(int a, int b) {
if(a%b==0) {
return b;
}
return getGcd(b, a%b);
}
}https://www.acmicpc.net/problem/1735
1735번: 분수 합
첫째 줄과 둘째 줄에, 각 분수의 분자와 분모를 뜻하는 두 개의 자연수가 순서대로 주어진다. 입력되는 네 자연수는 모두 30,000 이하이다.
www.acmicpc.net
'알고리즘 > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘]2458번: 키 순서_Java (0) | 2021.10.27 |
|---|---|
| [백준 알고리즘]1922번: 네트워크 연결_Java (0) | 2021.10.26 |
| [백준 알고리즘] 3955번: 캔디 분배_Java (0) | 2021.10.26 |
| [백준 알고리즘]1256번: 사전_Java (0) | 2021.10.03 |
| [백준 알고리즘]2143번: 두 배열의 합_Java (0) | 2021.10.03 |