쌉쌀한 무화과의 개발로그

문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/43162

📝문제

[문제 설명]

n	computers	return
3	[[1, 1, 0], [1, 1, 0], [0, 0, 1]]	2
3	[[1, 1, 0], [1, 1, 1], [0, 1, 1]]	1

입출력 예 설명

예제 #1
아래와 같이 2개의 네트워크가 있습니다.

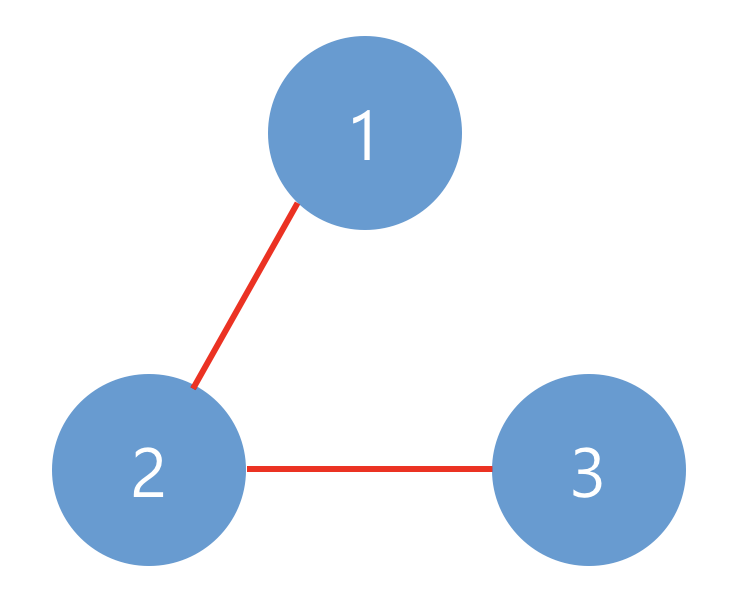
예제 #2
아래와 같이 1개의 네트워크가 있습니다.

📝풀이

bfs 풀이

import java.util.*;

class Solution {
    static boolean[] visit;
    static Queue<Integer> queue= new LinkedList<Integer>();
    
    public int solution(int n, int[][] computers) {
        int answer = 0;
        visit = new boolean[n];
        
        for(int i=0; i<n; i++){
            if(visit[i]) {
                continue;
            }
            answer++;
            bfs(computers, i, n);
        }
        
        return answer;
    }
    
    public void bfs(int[][] arr, int start, int len){
        int x;
        queue.offer(start);
        
        while(!queue.isEmpty()){
            x= queue.poll();
            
            for(int y=0; y<len; y++){
                if((arr[y][x]==1 || arr[x][y]==1) && !visit[y]){
                    visit[y]= true;
                    queue.offer(y);
                }
            }
        }
    }
}

반례

dfs / bfs 풀 때 보통 input 배열 기준으로 상하좌우로 움직이다보니, 처음에 이 문제를 잘못 이해했었는데요.

'프로그래머스 질문하기' 에서 어떤 분이 알려주신 반례로 문제를 다시 생각해보니 올바르게 이해가 되었습니다.

혹시 문제가 안풀리시는 분들 참고하세요.

[문제]

도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)

그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.

[입력]

첫째 줄에 컴퓨터의 수 N (1 ≤ N ≤ 1000)가 주어진다.

둘째 줄에는 연결할 수 있는 선의 수 M (1 ≤ M ≤ 100,000)가 주어진다.

셋째 줄부터 M+2번째 줄까지 총 M개의 줄에 각 컴퓨터를 연결하는데 드는 비용이 주어진다. 이 비용의 정보는 세 개의 정수로 주어지는데, 만약에 a b c 가 주어져 있다고 하면 a컴퓨터와 b컴퓨터를 연결하는데 비용이 c (1 ≤ c ≤ 10,000) 만큼 든다는 것을 의미한다. a와 b는 같을 수도 있다.

[출력]

모든 컴퓨터를 연결하는데 필요한 최소비용을 첫째 줄에 출력한다.

[예제]

[힌트]

이 경우에 1-3, 2-3, 3-4, 4-5, 4-6을 연결하면 주어진 output이 나오게 된다.

>문제 이해

모든 컴퓨터를 연결해야하는데,

- 가중치에 따라 최소 비용으로 모든 노선을 연결해야 한다.

​

만약 컴퓨터 a와 b가 연결되어있고, 컴퓨터 b와 c가 연결되어 있으면, a와 c가 연결되어 있다고 본다.

- 사이클이 없다.

​

=>> MST(Minimum Spanning Tree: 최소신장트리)의 특징이다.

​

​

​

>문제 풀이

union - find 베이스의 MST- 크루스칼 알고리즘으로 풀었다.

MST의 방법으로는 크루스칼과 프림이 있는데 이 문제에서는 간선의 개수가 적기 때문에 크루스칼 알고리즘을 이용해서 풀었다.

(크루스칼 알고리즘과 프림 알고리즘에 관한 간략한 차이를 아래에 적어놓았다.)

​

* 함수: union

: a와 b가 연결되어 있으면 둘의 부모를 같게 만들어 주는 과정

​

* 함수 find(int a)

: a의 조상을 찾아주는 과정이다. a와 b가 바로 연결이 안되어있어도 a의 조상과 b의 조상이 같으면 연결이 된거니까 이를 확인하기 위함이다.

​

* Main( )

priority queue를 이용해서 cost를 기준으로 input값들을 넣어준다.

그리고 이제 pq값들을 하나씩 꺼내서 최소비용으로 간선을 연결한다.

모든 노드를 연결해야하기 때문에 연결된 간선의 개수는 N-1이 되어야 한다.

간선을 연결할 때 마다 answer++ 카운팅을 해준다.

​

​

> 크루스칼 vs 프림

- 크루스칼

: 간선을 기준으로 선택해 나간다. 그래서 사이클이 이루어지는지 확인이 꼭 필요하다.

: 간선의 정렬이 오래 걸릴 수 있다. -> ∴ 간선이 적은 트리에 사용

- 프림

: 시작점을 기준으로 선택해 나가기 때문에 정점 중심 -> 사이클인지 아닌지 확인 할 필요가 없다.

>전체 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.io.IOException;
import java.util.Arrays;
import java.util.PriorityQueue;

public class Main {
	static int[] parent;
	static PriorityQueue<info> pq;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		int N, M;
		N= Integer.parseInt(br.readLine());
		M= Integer.parseInt(br.readLine());
		
		parent= new int[N+1];
		pq= new PriorityQueue<info>();
		for(int i=1; i<=N; i++) parent[i]= i;
		
		int start, target, cost;
		for(int i=0; i<M; i++) {
			st= new StringTokenizer(br.readLine());
			start= Integer.parseInt(st.nextToken());
			target= Integer.parseInt(st.nextToken());
			cost= Integer.parseInt(st.nextToken());
			//cost 순서로 최소힙 정렬
			pq.offer(new info(start, target, cost));
		}
		
		int answer=0, line=0;
		while(!pq.isEmpty()) {
			if(line==N-1) break;
			
			info cur= pq.poll();
			if(cur.start== cur.target) continue; //같은 컴은 연결필요X
			if(find(cur.start)!=find(cur.target)) {
				line++;
				union(cur.start, cur.target);
				answer+= cur.cost;
			}
		}
		System.out.println(answer);
	}//main
	
	//조상찾기
	static int find(int a) {
		if(parent[a]==a) return a;
		return find(parent[a]);
	}
	
	//동맹찾기
	static void union(int a, int b) {
		parent[find(a)]=find(b);
	}
	
	//노드 연결 정보
	static class info implements Comparable<info>{
		int start, target, cost;
		public info(int start, int target, int cost) {
			this.start= start;
			this.target= target;
			this.cost= cost;
		}
		@Override
		public int compareTo(info o) {
			return this.cost-o.cost;
		}
	}
}

https://www.acmicpc.net/problem/1922

[문제]

분수 A/B는 분자가 A, 분모가 B인 분수를 의미한다. A와 B는 모두 자연수라고 하자.

두 분수의 합 또한 분수로 표현할 수 있다. 두 분수가 주어졌을 때, 그 합을 기약분수의 형태로 구하는 프로그램을 작성하시오. 기약분수란 더 이상 약분되지 않는 분수를 의미한다.

[입력]

첫째 줄과 둘째 줄에, 각 분수의 분자와 분모를 뜻하는 두 개의 자연수가 순서대로 주어진다. 입력되는 네 자연수는 모두 30,000 이하이다.

​

[출력]

첫째 줄에 구하고자 하는 기약분수의 분자와 분모를 뜻하는 두 개의 자연수를 빈 칸을 사이에 두고 순서대로 출력한다.

[예제]

>문제 풀이

input))

분자1 분모1

분자2 분모2

​

이렇게 입력되면

c1/p1 과 c2/p2를 더하고 기약분수를 구해주면 됩니다.

나올 수 있는 최대수는 입력되는 분자 또는 분모가 30,000이하 이므로 9억 int 범위로 감당 가능합니다.

​

1) 분수의 합을 구하고

2) gcd를 구하여 기약분수를 만들어 출력한다.

​

gcd를 구할 때는 호제법을 사용한다.

​

​

> 유클리드 호제법이란?

gcd(A, B)= gcd(B, A%B)

​

* 증명

G를 A와 B의 최대공약수라고 할 때, A= aG, B= bG

A= Bq+r 니까

aG= bGq + r

r중심으로 정리하면 r = aG - bGq = (a-bq)G

B= bG , r= (a-bq)G 니까 G가 B와 r의 최대 공약수가 되려면 b와 (a-bq)가 서로소 임을 증명해야한다.

​

만약 서로소가 아니라고 가정을 해보자.

두 수가 서로소가 아니라면 b= mg , a-bq= ng 로 g라는 공약수가 존재한다.

b의 값을 오른쪽 식에 대입하면 a-mgq=ng

정리하면 a= (mq+n)g 이다.

​

우리는 처음에 A와 B 두 수를 A= aG, B= bG (G는 A와 B의 최대공약수) 라고 선언했는데, 즉 a와 b는 서로소라는 의미이다.

근데 아래 식에서 b= mg 이고 a= (mq+n)g 이면 a와 b는 공약수 g를 갖게된다.

따라서 b와 (a-bq)는 서로소이다.

​

​

>전체 코드

import java.util.Scanner;

public class Main {
	
	public static void main(String[] args) {
		Scanner scan= new Scanner(System.in);
		int c1, c2, p1, p2;
		
		//c1/p1, c2/p2
		c1= scan.nextInt();
		p1= scan.nextInt();
		c2= scan.nextInt();
		p2= scan.nextInt();
		
        //더해주고
		c1=c1*p2+c2*p1;
		p1=p1*p2;
		int gcd= getGcd(c1, p1); //최대공약수를 구해준다.
		
		System.out.println(c1/gcd+" "+p1/gcd); //기약분수 출력
	}//main
	
	public static int getGcd(int a, int b) {
		if(a%b==0) {
			return b;
		}
		return getGcd(b, a%b);
	}
}

https://www.acmicpc.net/problem/1735

[문제]

창영이는 선영이가 사탕을 공평하게 나누어주지 않으면 친구들을 때릴정도로 사탕을 좋아한다.

따라서, 선영이는 다음 파티에 사용할 사탕을 구매하기 전에 고민을 하기 시작했다.

만약 파티에 K명이 참가한다면, 공정하게 나누어주려면 K×X개를 사야 한다. (X는 자연수)

선영이는 항상 적어도 한 아이는 사탕을 잃어버린다는 사실을 알고 있다. 그래서 캔디를 하나 더 구매해 총 (K×X+1)개를 구매하려고 한다.

사탕은 봉지 단위로 판매한다. 한 봉지에는 사탕이 총 C개 들어있다. 문제의 조건을 만족하면서 구매할 수 있는 사탕 봉지의 개수를 구하는 프로그램을 작성하시오.

[입력]

첫째 줄에 테스트 케이스의 개수 t가 주어진다. (0 < t < 100) 각 테스트 케이스는 한 줄로 이루어져 있고, K와 C가 공백으로 구분되어져서 주어진다. (1 ≤ K, C ≤ 109) 선영이는 부자가 아니기 때문에 109개를 넘는 사탕 봉지를 구매하지 못한다.

[출력]

각 테스트 케이스에 대해서 문제의 조건을 만족시키면서 구매할 수 있는 사탕 봉지가 없다면, "IMPOSSIBLE"을 출력한다. 이 경우가 아닌 경우에는 선영이가 구매해야 하는 사탕 봉지의 수를 출력한다. 만약, 가능한 봉지의 수가 여러개라면 아무거나 출력한다.

[예제]

>문제 풀이

창영이는 사탕을 좋아한다.

선영이는 구매하기 전에 고민을 시작했다.

만약, K명이 참가한다면, 공정하게 K x X(자연수) 사야한다.

항상 한 아이는 사탕을 잃어버린다.

그래서 (K x X + 1) 개를 구매해야한다.

사탕은 봉지 단위로 판매한다.

사탕은 총 C개 들어있다.

몇 봉지를 사야하는가?

​

input))

t     //(0<t<100)

K C  //(1<=K, C<=10^9)

​

output))

만족하는 사탕 봉지가 없다면, "IMPOSSIBLE"

여러개면 아무거나 출력

​

즉, K와 C가 주어지고 x: 인당 나눠줄 사탕 개수, y: 구매할 사탕 봉지 개수 라고 할때,

-Kx+Cy=1 을 만족하는 y를 찾아야한다.

​

* X의 시작점은 K/C의 올림수=> (int)(K+1)/C

​

>문제 풀이

gcd를 구할 때 유클리드 호제법을 쓴다면, 일차방정식의 해를 구할 때는 확장된 유클리드 호제법을 사용할 수 있다.

​

​

확장된 유클리드 호제법 설명 참고: https://sexycoder.tistory.com/65

>전체 코드

import java.util.Scanner;

public class Main {
	
	public static void main(String[] args) {
		int N, K, C;
		Scanner scan= new Scanner(System.in);
		
		N= scan.nextInt();
		for(int i=0; i<N; i++) {
			K= scan.nextInt();
			C= scan.nextInt();
			long x0, y0;
			
			EGResult result= extendedGcd(K, C);
			if(result.r!=1) {
				System.out.println("IMPOSSIBLE");
			}else {
				x0= result.s;
				y0= result.t;
				
				y0%=K;
				if(y0<0) y0+=K;
				y0= Math.max(y0, (K+C)/C);
				if(y0<= 1e9) {
					System.out.println(y0);
				}else {
					System.out.println("IMPOSSIBLE");
				}
			}
		}
	}//main

	public static EGResult extendedGcd(long a, long b) {
		long s0=1, t0=0, r0=a;
		long s1=0, t1=1, r1=b;
		
		long temp;
		while(r1!=0) {
			long q= r0/r1;
			
			temp= r0 - q*r1;
			r0= r1;
			r1= temp;
			
			temp= s0 - q*s1;
			s0= s1;
			s1= temp;
			
			temp= t0 - q*t1;
			t0= t1;
			t1= temp;
		}
		return new EGResult(s0, t0, r0);
	}//EGResult
	
	static class EGResult{
		long s, t, r;
		public EGResult(long s, long t, long r) {
			super();
			this.s= s;
			this.t= t;
			this.r= r;
		}
	}//EGResult
}

https://www.acmicpc.net/problem/3955

[문제]

체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?

[입력]

입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.

각 테스트 케이스는 세 줄로 이루어져 있다. 첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다. 체스판의 크기는 l × l이다. 체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다. 둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.

[출력]

각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.

[예제]

>문제 풀이

 기존에 한칸 씩 이동하던 BFS문제에서 이동 거리만 조정해주면 되는 문제였습니다.

해설할게 없는,, 문제랄까,,?

>전체 코드

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
	static int T, l, mat[][];
	static boolean visited[][];
	
	public static void main(String [] args) {
		int x, y, dst_x, dst_y;
		
		Scanner scan= new Scanner(System.in);
		
		T= scan.nextInt();
		while(T-->0){
			l= scan.nextInt();
			x= scan.nextInt();
			y= scan.nextInt();
			dst_x= scan.nextInt();
			dst_y= scan.nextInt();
			
			mat= new int[l][l];
			visited= new boolean[l][l];
			
			visited[x][y]=true;
			
			bfs(x, y, dst_x, dst_y);
		}
		
	}
	
	public static void bfs(int x, int y, int dst_x, int dst_y) {
		int nx, ny;
		int dx[]= {-1, -2, 1, 2, 2, 1, -2, -1};
		int dy[]= {-2, -1, -2, -1, 1, 2, 1, 2};
		
		Queue<Integer> que= new LinkedList<Integer>();
		que.offer(x);
		que.offer(y);
		
		while(!que.isEmpty()) {
			x= que.poll();
			y= que.poll();
			
			if(x==dst_x&&y==dst_y) {
				System.out.println(mat[x][y]);
				return;
			}
			for(int i=0; i<8; i++) {
				nx= x+dx[i];
				ny= y+dy[i];
				
				if(nx<0||nx>=l||ny<0||ny>=l) continue;
				
				if(mat[nx][ny]==0&&!visited[nx][ny]) {
					visited[nx][ny]=true;
					mat[nx][ny]= mat[x][y]+1;
					que.offer(nx);
					que.offer(ny);
				}
			}
			
		}//while
	}//bfs
	
}

www.acmicpc.net/problem/7562