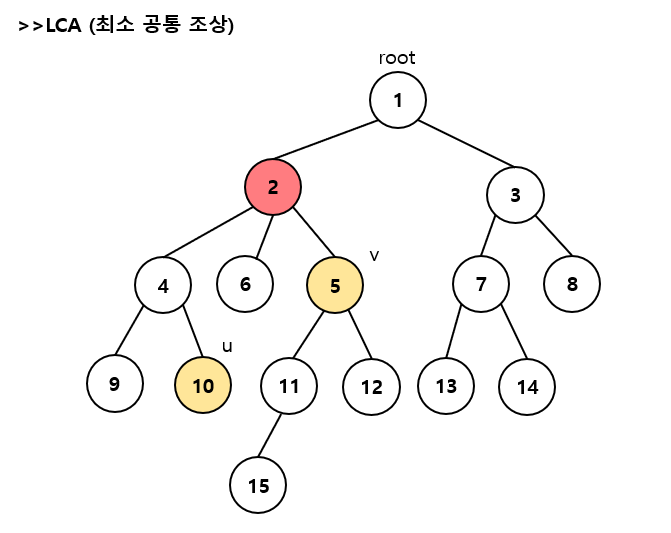
[문제]
우리는 스마트폰을 사용하면서 여러 가지 앱(App)을 실행하게 된다. 대개의 경우 화면에 보이는 ‘실행 중’인 앱은 하나뿐이지만 보이지 않는 상태로 많은 앱이 '활성화'되어 있다. 앱들이 활성화 되어 있다는 것은 화면에 보이지 않더라도 메인 메모리에 직전의 상태가 기록되어 있는 것을 말한다. 현재 실행 중이 아니더라도 이렇게 메모리에 남겨두는 이유는 사용자가 이전에 실행하던 앱을 다시 불러올 때에 직전의 상태를 메인 메모리로부터 읽어 들여 실행 준비를 빠르게 마치기 위해서이다.
하지만 스마트폰의 메모리는 제한적이기 때문에 한번이라도 실행했던 모든 앱을 활성화된 채로 메인 메모리에 남겨두다 보면 메모리 부족 상태가 오기 쉽다. 새로운 앱을 실행시키기 위해 필요한 메모리가 부족해지면 스마트폰의 운영체제는 활성화 되어 있는 앱들 중 몇 개를 선택하여 메모리로부터 삭제하는 수밖에 없다. 이러한 과정을 앱의 ‘비활성화’라고 한다.
메모리 부족 상황에서 활성화 되어 있는 앱들을 무작위로 필요한 메모리만큼 비활성화 하는 것은 좋은 방법이 아니다. 비활성화된 앱들을 재실행할 경우 그만큼 시간이 더 필요하기 때문이다. 여러분은 이러한 앱의 비활성화 문제를 스마트하게 해결하기 위한 프로그램을 작성해야 한다
현재 N개의 앱, A1, ..., AN이 활성화 되어 있다고 가정하자. 이들 앱 Ai는 각각 mi 바이트만큼의 메모리를 사용하고 있다. 또한, 앱 Ai를 비활성화한 후에 다시 실행하고자 할 경우, 추가적으로 들어가는 비용(시간 등)을 수치화 한 것을 ci 라고 하자. 이러한 상황에서 사용자가 새로운 앱 B를 실행하고자 하여, 추가로 M 바이트의 메모리가 필요하다고 하자. 즉, 현재 활성화 되어 있는 앱 A1, ..., AN 중에서 몇 개를 비활성화 하여 M 바이트 이상의 메모리를 추가로 확보해야 하는 것이다. 여러분은 그 중에서 비활성화 했을 경우의 비용 ci의 합을 최소화하여 필요한 메모리 M 바이트를 확보하는 방법을 찾아야 한다.
[입력]
입력은 3줄로 이루어져 있다. 첫 줄에는 정수 N과 M이 공백문자로 구분되어 주어지며, 둘째 줄과 셋째 줄에는 각각 N개의 정수가 공백문자로 구분되어 주어진다. 둘째 줄의 N개의 정수는 현재 활성화 되어 있는 앱 A1, ..., AN이 사용 중인 메모리의 바이트 수인 m1, ..., mN을 의미하며, 셋째 줄의 정수는 각 앱을 비활성화 했을 경우의 비용 c1, ..., cN을 의미한다
단, 1 ≤ N ≤ 100, 1 ≤ M ≤ 10,000,000이며, 1 ≤ m1, ..., mN ≤ 10,000,000을 만족한다. 또한, 0 ≤ c1, ..., cN ≤ 100이고, M ≤ m1 + m2 + ... + mN이다.
[출력]
필요한 메모리 M 바이트를 확보하기 위한 앱 비활성화의 최소의 비용을 계산하여 한 줄에 출력해야 한다.
[예제]

>문제 풀이
유명한 배낭 알고리즘을 이용해서 풀어야하는 문제였습니다.
* 변수 설명
N // 입력되는 앱의 개수
M //필요한 메모리의 양
App apps[]; //앱을 저장할 객체 배열 App(int memory, int cost)
int dp[]; //dp[i]: 비용 i를 사용할때 비울 수 있는 최대 메모리
* 로직
for ( int i: 0~N ) {
for( int j: costSum~apps[i].cost ){
dp[j]= Math.max( dp[j], dp[j-apps[i].cost]+apps[i].mem );
}
}
cost로 만들 수 있는 최대 메모리를 매번 구할 수 없기 때문에 dp 배열에 memoization해줍니다.
| mem / cost(→) | j-i | j |
| dp[cost] :cost로 만들수 있는 최대 메모리 |
dp[j-i] | dp[j]=?? |
dp[j]= Math.max( dp[j], dp[j-apps[i].cost] + apps[i].mem );
dp[j]에 dp[j] 값이랑 ( j비용에서 i번째 앱의 비용을 뺀 비용으로 만들 수 있는 최대 메모리) + i번째 앱의 메모리 중 큰 값을 넣습니다.
>전체 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.io.IOException;
public class Main {
public static void main(String [] args) throws IOException {
int N, M, costSum=0; //N: input 개수, M: 원하는 메모리값
App apps[]; //input
int dp[]; //cost가 i일때 최대 메모리
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st= new StringTokenizer(br.readLine());
StringBuilder sb= new StringBuilder();
//1. 입력받기
N= Integer.parseInt(st.nextToken());
M= Integer.parseInt(st.nextToken());
apps=new App[N];
//1-1. set Mem
st= new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
apps[i]= new App(0, 0);
apps[i].setMemory(Integer.parseInt(st.nextToken()));
}
//1-2. set Cost
st= new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
apps[i].setCost(Integer.parseInt(st.nextToken()));
costSum+= apps[i].getCost();
}
dp= new int[costSum+1];
//2. napsack 알고리즘
for(int i=0; i<N; i++) {
for(int j=costSum; j>=apps[i].getCost(); j--) {
dp[j]= Math.max(dp[j], dp[j-apps[i].getCost()]+apps[i].getMemory());
}
}
//3. M이상 메모리를 확보하기 위한 비용 i 출력
for(int i=0; i<=costSum; i++) {
if(dp[i]>=M) {
System.out.println(i);
break;
}
}
}
static class App{
int memory;
int cost;
public App(int memory, int cost) {
this.memory = memory;
this.cost = cost;
}
public int getMemory() {
return memory;
}
public void setMemory(int memory) {
this.memory = memory;
}
public int getCost() {
return cost;
}
public void setCost(int cost) {
this.cost = cost;
}
}//class App
}https://www.acmicpc.net/problem/7579
7579번: 앱
입력은 3줄로 이루어져 있다. 첫 줄에는 정수 N과 M이 공백문자로 구분되어 주어지며, 둘째 줄과 셋째 줄에는 각각 N개의 정수가 공백문자로 구분되어 주어진다. 둘째 줄의 N개의 정수는 현재 활
www.acmicpc.net
'알고리즘 > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘]1072번: 게임_Java (0) | 2021.09.30 |
|---|---|
| [백준 알고리즘]1713번: 후보 추천하기_Java (0) | 2021.09.30 |
| [백준 알고리즘]2449번: 전구_Java (0) | 2021.09.30 |
| [백준 알고리즘]11659번: 구간 합 구하기4_Java (0) | 2021.09.30 |
| [백준 알고리즘]11438번: LCA 2_Java (0) | 2021.09.30 |